A Simple Method to Estimate Movement Deviation

A Hopefully Correct Methodology

I am terrible at physics, so who better than I to postulate a simple methodology to estimate movement deviation? As with all my work, but especially any of my work which pertains to physics, note that I’m not an expert, so there may be errors in my understanding and/or methodology. Should you find any errors, please let me know, I’ll be delighted to correct my understanding.

What is movement deviation? Simply put, it’s the difference between movement that we’d expect given just spin, compared to the movement we actually observed.

Let’s begin with a simple illustration:

Statcast reports a spin axis, which is measured by HawkEye. A spin axis of 90° would indicate movement that is purely horizontal, in the direction of a left-handed batter. Similarly, a 270° spin axis would also be purely horizontal, but towards a right-handed batter. A 4 seam fastball with pure backspin would have a spin axis of 180°, while a curveball with pure topspin would have an axis of 0° or 360°, whichever you prefer to use. Practically speaking, that means we can translate the spin axis into a unitized spin, such that x² + z² = 1. Here’s how to do it:

Translating the spin axis into X and Z movement:

Spin Z = -Cos(Spin Axis)
Spin X = Sin(Spin Axis)

If you’re doing it in Excel, and probably most programming languages, you’ll need to convert to radians first. This is simply SIN(RADIANS(Spin Axis)) for the x spin component. To make sure we standardize for RHP, I mutliply by -1 for RHPs and keep the number the same for LHPs (only for the X/horizontal component).

Total Movement

Let’s start with the simplest possible way to apply this methodology. We’re going to measure the total induced movement:

Total Movement = SQRT(IVB²+HB²)

That means if a pitch has 20” of IVB and 10” of HB, it will have 22.36” of total movement. Now we’re going to make a very critical assumption, which is probably very incorrect, but will be quite useful in practice:

Assumption: The non-spin movement factors do not materially increase or decrease the total movement, but they change the x and z proportions. This is likely incorrect, however, it should serve to give us a general idea of the magnitude of the movement deviation.

Spin Z and Spin X Movement

Let’s assume our 20” IVB / 10” HB pitch was thrown with a 225° spin axis, this will imply 0.707 of each inch of total movement will be horizontal, and 0.707 of each inch of total movement will be vertical. That would mean that the spin axis, for a pitch that moved a total of 22.36”, would have 15.81” of IVB and 15.81” of HB.

If you take the total movement of 15.81 and 15.81, you’ll end up with 22.36”. This is essentially saying, if we assumed all of the movement was just spin based, we’d see 15.8/15.8, but what we actually saw was 20/10. That means we saw +4.2” of IVB deviation, and -5.8” of HB deviation.

This is similar in spirit to spin axis shift, but it gives us a useful magnitude as well. Do we care if a gyro slider with essentially 0/0 movement has 120° of spin axis shift? Not really. But I care a lot if a sinker’s spin axis says it should get 8” of IVB, given the total movement, but it only gets 0” of IVB.

Again, this relies on an assumption that won’t be entirely correct, but I think provides a practical, intuitive lens for measuring movement deviation. It’s likely that SSW is an additive effect, such that say total movement by spin is 20”, but the SSW added 4” of total movement (or killed 4” of vertical movement if we went the other way), which would mean the total movement was only 16” for the non-SSW movement. This is beyond my skill level to estimate properly, but I imagine this would be possible given the pitch type efficiency numbers you can find on Savant.

Let’s Drag This Out a Bit

Dr. Nathan’s spreadsheets, which this work builds upon, would estimate movement without drag in order to calculate the inferred spin axis based on movement. In the spreadsheet that I provide these are simply labelled x_mvmt and z_mvmt.

You can download the Excel file here: Smoke Spreadsheet

This will apply the same methodology, but will calculate total movement, while adjusting for drag. Is that a “better” way to do it? I really don’t know. I’d love it if someone compared the “simple” version vs the slightly more complicated version which requires a few extra steps.

I highly encourage you to download the spreadsheet, and build it out for yourself.

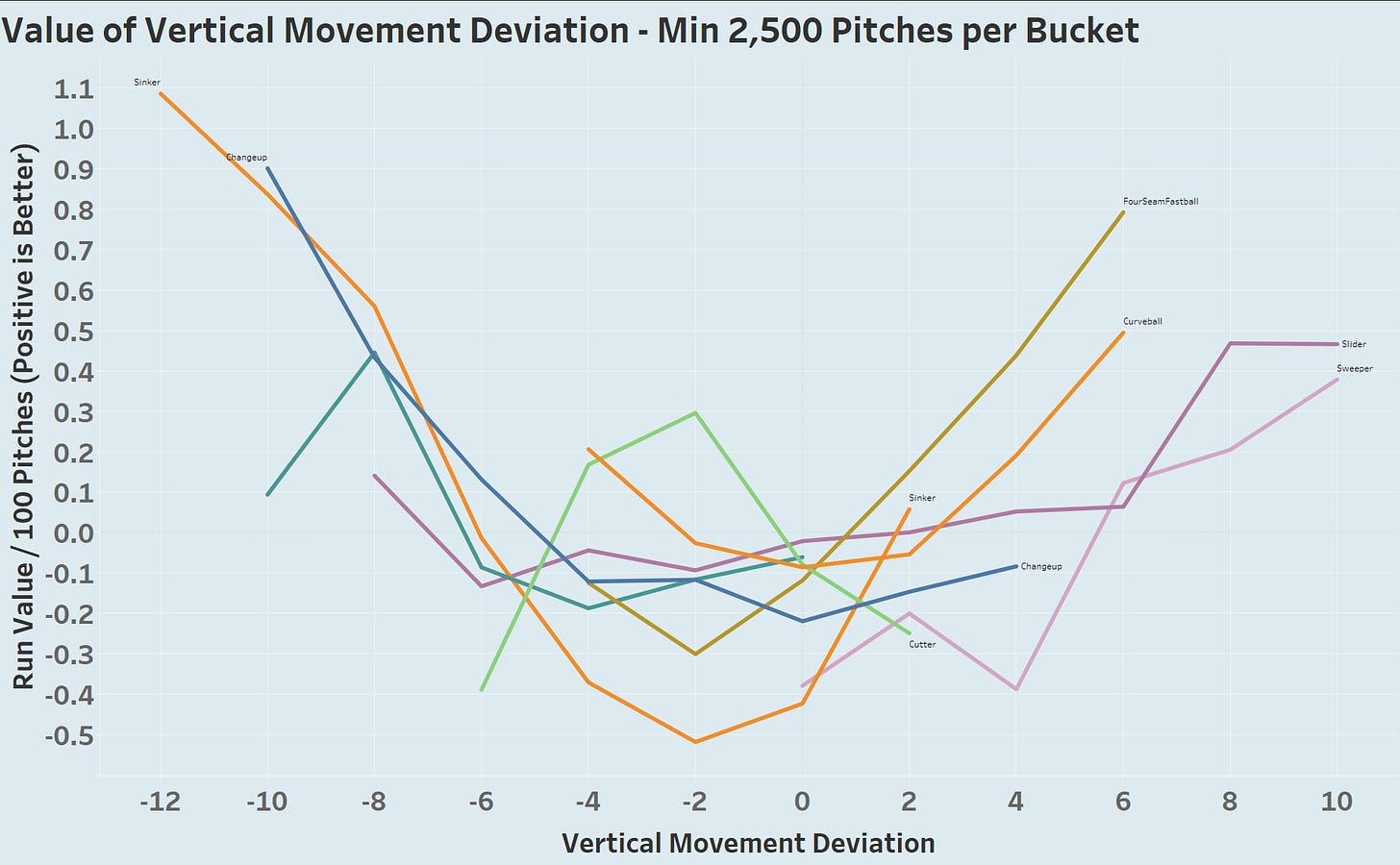
We see a clear relationship to vertical movement deviation and the quality of sinkers and changeups.

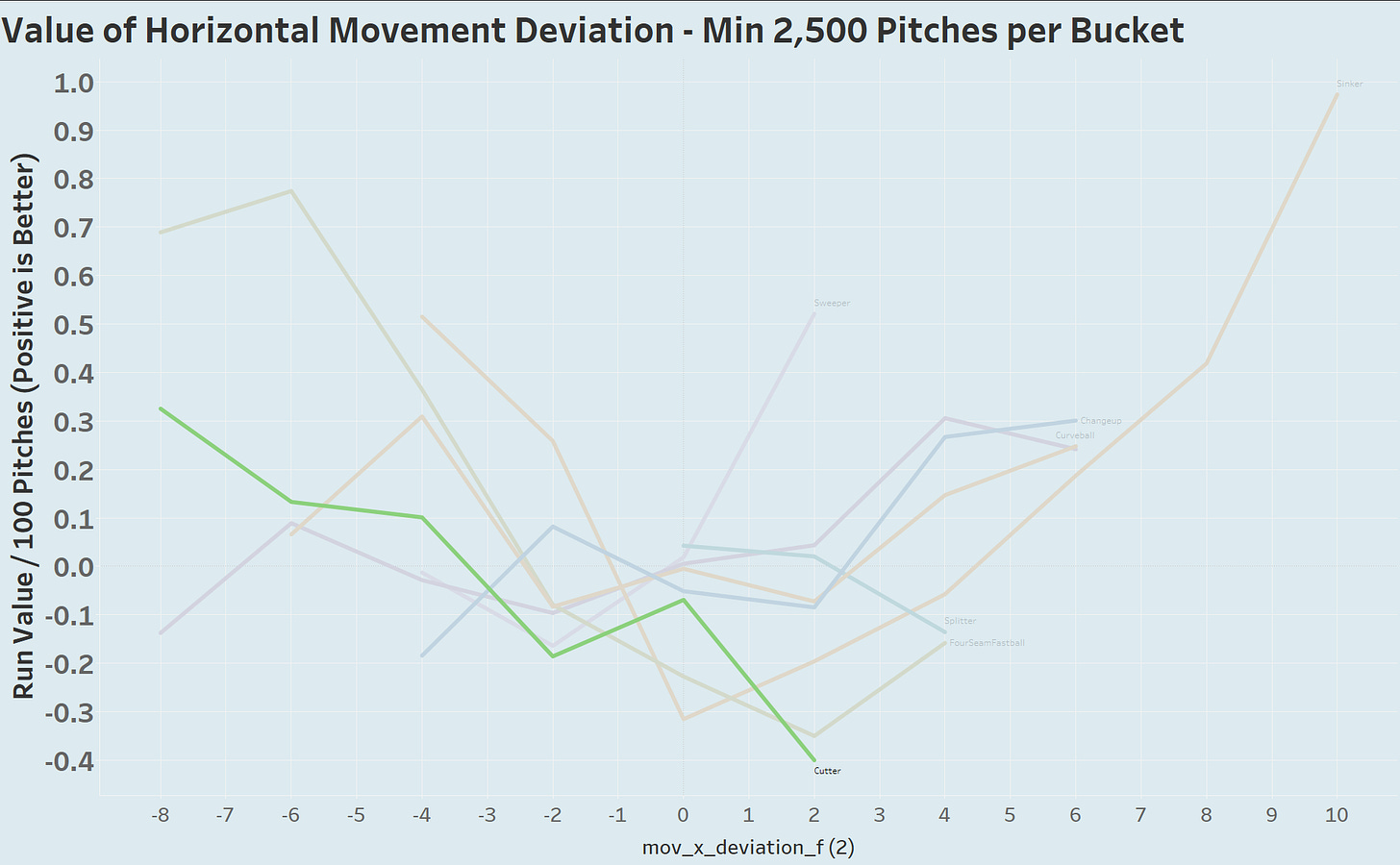
We can also see the importance of a cutter getting non-spin induced cutting action. It’s a wonderfully useful lens to describe pitches, perhaps glean some hints at their value, and also to identify pitchers with the skill to create large magnitude movement deviation.

Concluding Thoughts

I sincerely hope this methodology is useful to you. It took a lot of fumbling in the dark for me to figure this out. The data this methodology produces are consistent with my understanding of the game, so while I’ll never be fully confident that this is a correct way of capturing movement deviation, I’m quite confident it is a valuable lens to look at pitch shapes.

If you build a better version, please let me know, I’ll be delighted.